A Estatística é o estudo da coleta, análise, interpretação, apresentação, organização e utilização de dados. É uma disciplina interdisciplinar que utiliza métodos matemáticos, computacionais e teóricos para resolver problemas relacionados a decisões baseadas em dados. A Estatística é amplamente aplicada em muitas áreas, incluindo ciências sociais, ciências da saúde, economia, ciências da computação, ciências biológicas, entre outras.
O objetivo principal da Estatística é ajudar as pessoas a tomar decisões informadas a partir de dados, fornecendo métodos para estimar incertezas e avaliar riscos. Além disso, a Estatística também é usada para descrever e compreender padrões e tendências nos dados, bem como para testar hipóteses e fazer previsões.
O que é Estatística Descritiva?
A Estatística Descritiva é o ramo da estatística que visa sumarizar e descrever qualquer conjunto de dados. Em outras palavras, é aquela estatística que está preocupada em sintetizar os dados de maneira direta, preocupando-se menos com variações e intervalos de confiança dos dados. Exemplos de estatísticas descritivas são a média, o desvio padrão e a mediana.
Agora eu te pergunto: você domina os conceitos de estatística descritivas simples que estamos tão acostumados a ver no dia a dia? Média, mediana, desvio padrão, variância, etc? Se sua resposta é não, ou mais ou menos, este post vai te ajudar! Aqui, temos como objetivo apresentar esses conceitos de forma simples e aprofundar-se um pouco mais em cada um deles.

Para que a Estatística descritiva é usada?
Sumarizar dados
Resumir e descrever dados em um formato compreensível. Por exemplo, ela pode ser usada para calcular médias, medianas, modas, desvios padrão e outras medidas resumidas para um conjunto de dados.
Comparar grupos
Comparar características importantes de grupos diferentes. Por exemplo, ela pode ser usada para comparar a média de idade de homens e mulheres em uma população.
Visualizar dados
Criar gráficos e visualizações que ajudam a entender os dados. Por exemplo, ela pode ser usada para criar um histograma para mostrar a distribuição de uma variável em um conjunto de dados.
Identificar padrões
Identificar padrões nos dados. Por exemplo, ela pode ser usada para identificar outliers ou valores atípicos em um conjunto de dados.
O que são as Medidas de Centralidade na Estatística Descritiva?
As Medidas de Centralidade são os procedimentos gráficos apresentados até agora no blog. Sua função é basicamente ajudar a visualizar a forma da distribuição das medidas, como é o caso do histograma. O próximo passo na análise é quantificar alguns aspectos importantes da distribuição. Duas medidas são amplamente utilizadas: uma para localizar a posição central e outra para quantificar a variabilidade ou dispersão da distribuição.
A medida de posição central é um valor representativo da distribuição em torno do qual as outras medidas se distribuem. Duas medidas são as mais utilizadas: a média aritmética e a mediana.
O que é uma Média Aritmética na Estatística Descritiva?
A média aritmética de um conjunto de n valores é obtida somando-se todas as medidas e dividindo a soma por n. Representamos cada valor individual por uma letra (x, y, z, etc.), seguida por um sub-índice, ou seja, representamos os n valores da amostra por x1, x2, x3, ..., xn, na qual x1 é a primeira observação, x2 é a segunda e assim por diante. Então, escrevemos:
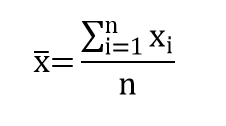
Considere S um símbolo matemático do qual se lê "somatório" de xi, para i variando de 1 a n, que é equivalente a x1 + x2 + x3 +...+xn.
Confira um exemplo:
Em um grupo de cinco pessoas, com idades de 19, 23, 25, 28 e 29 anos, qual é a Média Aritmética de suas idades?
Primeiramente, é preciso somar suas idades:
19 + 23 + 25 + 28 + 29 = 124
Em seguida, divide-se essa soma pelo número de "fontes de dados" (ou pessoas, se preferir). Veja:
(19 + 23 +25 +28 + 29)/ 5 → 124/5 = 24,8
Dessa forma, obtemos que a Média Aritmética (ou simplesmente Média) da idade desse grupo é de 24,8 anos. Percebe que não é uma conta difícil de fazer?
O que é a Mediana na Estatística Descritiva?
A Mediana é uma medida alternativa à Média Aritmética e sua função é representar o centro da distribuição, muito usada em estatística descritiva. A mediana de um conjunto de medidas (x1, x2, x3, ..., xn) é um valor M tal que pelo menos 50% das medidas são menores ou iguais a M e pelo menos 50% das medidas são maiores ou iguais a M. Em outras palavras, 50% das medidas ficam abaixo da mediana e 50% acima desse valor.
Confira um exemplo:
Uma mulher, durante seu período reprodutivo, deu à luz 5 crianças. Os pesos dos recém-nascidos foram, respectivamente: 9.2, 6.4, 10.5, 8.1 e 7.8. Calcule a mediana dos pesos.
Os valores, ordenados do menor para o maior, são:
6.4 7.8 8.1 9.2 10.5.
Portanto, a mediana é 8.1 kg.
Agora veja outro exemplo, um pouco diferente:
Os dados abaixo são tempos de vida (em dias) de 8 lâmpadas:
500 550 550 550 600 700 750 2000
Note que temos dois valores que satisfazem a condição de ser mediana, o quarto (550) e o quinto (600), já que a quantidade de valores corresponde a um número par. Nesse caso, definimos a Mediana como sendo a Média dos dois valores centrais:
(550 + 600)/2 → 1150/2 = 575
Vale destacar: Observe que se a lâmpada que sobreviveu 2000 dias tivesse sobrevivido 3950 dias, o valor da mediana não se alteraria. Por outro lado, a média aritmética aumentaria. Não ser afetada por valores extremos é uma vantagem da mediana em relação à média. Quando a distribuição dos dados é simétrica, os valores da média e da mediana praticamente coincidem. Mas, quando a distribuição é assimétrica, a média é "puxada" na direção da assimetria.
Quase sempre, quando olhamos uma média, fazemos algum julgamento de valor. Por exemplo: se lemos no jornal qual é a renda média de uma determinada comunidade, somos tentados a avaliar como é a situação econômica dessa comunidade. No entanto, o valor da média pode ser alto e, mesmo assim, a situação social ser muito ruim. Basta que poucos ganhem muito e muitos ganhem pouco. A mediana, por outro lado, não é influenciada por esses valores extremos e, nesse caso, refletirá melhor a condição econômica da comunidade.
Por isso que, em qualquer estudo, é interessante reportar as duas medidas de centralidade.
O que é Moda na estatística descritiva?
A Moda de uma distribuição é o valor que ocorre com mais frequência ou o valor que corresponde ao intervalo de classe com a maior frequência. Assim a moda, da mesma forma que a Mediana, não é afetada por valores extremos.
Uma distribuição de frequência que apresenta apenas uma moda é chamada de unimodal. Já se a distribuição apresenta dois pontos de alta concentração, ela é chamada de bimodal. Distribuições bimodais ou multimodais podem indicar que na realidade a distribuição de frequência se refere a duas populações cujas medidas foram misturadas.
Por exemplo, suponha que um lote de caixas de leite longa vida passa por um processo de amostragem e em cada caixa da amostra é medido o volume envasado. Se o lote é formado pela produção de duas máquinas de envase que estão calibradas em valores diferentes, é possível que o histograma apresente duas modas: uma para cada valor de calibração.
O que são os Percentis (ou Quartis)?
Se o número de dados observados é grande, é interessante calcular algumas outras medidas de posição. Essas medidas são uma extensão do conceito de mediana.
Suponha que estamos conduzindo um experimento com animais. Eles recebem uma droga e medimos o tempo de vida (em dias) após a ingestão dessa droga. Poderíamos fazer a seguinte pergunta: em quanto tempo 50% dos animais ainda estão vivos? Obviamente esse valor será a mediana.
Por outro lado, poderíamos estar interessados em saber qual é o tempo em que 75%, ou 25%, dos animais estão vivos. Esses valores são chamados de Quartis da distribuição (pois dividem a distribuição em quartas partes) e são representados por Q1 (1º quartil – 25%) e Q3 (3º quartil – 75%). O segundo quartil, Q2, que corresponde a 50%, é a mediana.
Esse conceito pode ser estendido um pouco mais e, em lugar de 25%, 50% e 75%, poderíamos querer calcular percentis (5%,10%, 90%, etc.).
Seja p um número qualquer entre 0 e 1. O 1100×p-ésimo percentil é um valor tal que, depois de as medidas terem sido ordenadas, pelo menos 100×p% das medidas são menores ou iguais a esse valor. E pelo menos 100×(1-p)% das medidas são maiores ou iguais a esse valor.
Exemplo: O ganho de peso, em gramas, de 9 ratos submetidos a uma dieta são dados a seguir:
93.9 105.8 106.5 116.6 125.0 128.3 132.1 136.7 152.4
Como calcular o primeiro e o terceiro quartis?
Cálculo de Q1:
Q1 corresponde a 25%. Então, p = 0.25 .
O número de observações menores ou iguais a Q1 é 0.25 × 9 = 2.25.
O número de observações maiores ou iguais a Q1 é (1-0.25) × 9 → 0.75 × 9 = 6.75
Em outras palavras, pelo menos 3 observações têm que ser menores ou iguais a Q1 e pelo menos 7 observações têm que ser maiores ou iguais a Q1. A medida 106.5 satisfaz esses requerimentos. Portanto, Q1 = 106.5.
Cálculo de Q3:
Argumentos semelhantes mostram que Q3 = 132.1.
Temos também que Q2 = 125.0, que é a Mediana.
Exemplo:
Calcular os quartis e os percentis 5%, 10%, 90% e 95% para o amostra de valor de venda de um produto em 95 pontos de venda amostrados apresentado acima.
75% Q3 45.3 5% 35.2
50% Q2 42.2 10% 37.0
25% Q1 39.5 90% 47.0
Média 42.4 95% 50.2
Como fazer Cálculos Estatísticos rápidos?
Softwares de Análise Estatística calculam percentis e outras estatísticas descritivas utilizando diferentes métodos, os quais envolvem algum tipo de interpolação. Por isso, é possível encontrar discrepâncias entre os valores calculados por diferentes programas. Mas essas discrepâncias em geral não afetam a análise.
Quais são os tipos de estatísticas?
Existem vários tipos de estatísticas, mas alguns dos principais incluem:
- Estatística descritiva: é o ramo da estatística que se concentra na coleta, organização, análise, interpretação e apresentação de dados.
- Estatística inferencial: é o ramo da estatística que se concentra na generalização a partir de amostras para inferir informações sobre uma população.
- Probabilidade: é a área da estatística que se concentra em estudar as probabilidades de eventos aleatórios.
- Análise de variância: é uma técnica estatística que compara duas ou mais médias de grupos para determinar se há diferenças significativas entre elas.
- Regressão: é uma técnica estatística que permite prever uma variável dependente a partir de uma ou mais variáveis independentes.
- Correlação: é uma medida da relação linear entre duas variáveis quantitativas.
- Estatísticas de tendência central: incluem média, mediana e moda, e são usadas para descrever o comportamento central de um conjunto de dados.
- Estatísticas de dispersão: incluem variância e desvio padrão, e são usadas para descrever a variabilidade de um conjunto de dados.
Como interpretar os resultados estatísticos e fazer conclusões a partir dos dados?
Verifique se os dados foram coletados e processados corretamente
Antes de começar a analisar os dados, é importante garantir que eles tenham sido coletados e processados corretamente. Isso inclui verificar se os dados estão completos, se há erros de digitação ou outras inconsistências, e se foram aplicados os procedimentos adequados para lidar com valores ausentes ou discrepantes.
Faça uma análise descritiva dos dados
Antes de fazer qualquer inferência, é importante ter uma compreensão geral dos dados. Isso pode incluir a construção de tabelas de frequência, gráficos, cálculo de medidas de tendência central (média, mediana, moda) e medidas de dispersão (desvio padrão, intervalos interquartis). A análise descritiva pode ajudar a identificar padrões, tendências e valores atípicos nos dados.
Determine a distribuição dos dados
A distribuição dos dados pode ajudar a determinar qual técnica estatística é mais apropriada para analisar os dados. Algumas técnicas estatísticas, como o teste t e a análise de variância, requerem uma distribuição normal dos dados.
Faça inferências estatísticas
Com base na distribuição dos dados, pode-se realizar uma variedade de testes estatísticos para fazer inferências sobre a população a partir da amostra. Isso pode incluir testes de hipóteses, intervalos de confiança e análises de regressão.
Faça conclusões a partir dos resultados
Finalmente, as conclusões devem ser baseadas nos resultados das análises estatísticas. É importante lembrar que as conclusões são baseadas em evidências e não são garantidas. Portanto, as conclusões devem ser interpretadas com cautela, levando em consideração a precisão dos dados, as limitações do estudo e outras fontes de incerteza.
Como usar a estatística para tomar decisões e resolver problemas de negócios?
Análise de dados
A estatística pode ajudar a analisar grandes conjuntos de dados para identificar tendências, padrões e insights que podem ajudar a tomar decisões informadas de negócios. A análise de dados pode ser usada em várias áreas, como marketing, vendas, finanças e operações.
Previsão
A estatística pode ser usada para prever tendências futuras com base em dados históricos. Isso pode ajudar a tomar decisões informadas sobre orçamento, investimentos, estratégia de marketing e muito mais.
Controle de qualidade
A estatística pode ser usada para monitorar a qualidade dos produtos ou serviços de uma empresa. Isso pode envolver a análise de dados de teste para identificar problemas de qualidade e implementar melhorias no processo.
Pesquisa de mercado
A estatística pode ser usada para coletar e analisar dados de pesquisa de mercado. Isso pode ajudar a entender as necessidades dos clientes, identificar oportunidades de mercado e avaliar a eficácia de campanhas de marketing.
Análise de risco
A estatística pode ser usada para avaliar o risco de uma decisão de negócios. Isso pode envolver a análise de dados financeiros, histórico de desempenho da empresa e outros fatores relevantes para avaliar o risco associado a uma determinada decisão.
Como evitar erros comuns na análise estatística?
Entender os dados
Antes de começar a análise, é importante ter uma compreensão clara dos dados que serão analisados, incluindo o tipo de dados, a escala de medida e quaisquer limitações ou tendências nos dados.
Selecionar a técnica de análise apropriada
É importante selecionar a técnica de análise apropriada com base no tipo de dados e na pergunta de pesquisa. Usar a técnica errada pode levar a resultados imprecisos ou inválidos.
Verificar a normalidade dos dados
Antes de realizar a análise, é importante verificar se os dados estão normalmente distribuídos. Isso pode ser feito por meio de gráficos e testes estatísticos, como o teste de normalidade de Shapiro-Wilk.
Verificar a independência dos dados
É importante verificar se os dados são independentes uns dos outros. Isso é especialmente importante em análises de regressão, onde a violação da independência pode levar a resultados incorretos.
Verificar a homogeneidade das variâncias
Em análises que envolvem comparações entre grupos, é importante verificar se as variâncias dos grupos são homogêneas. A violação da homogeneidade pode levar a resultados incorretos ou imprecisos.
Realizar uma análise adequada de outliers
Outliers são valores extremos que podem afetar a análise. É importante determinar se esses valores são erros ou se representam uma parte real dos dados. Em caso de outliers verdadeiros, pode ser necessário usar técnicas de análise robustas para minimizar seu efeito.
Verificar a significância estatística
É importante verificar se os resultados são estatisticamente significativos. Isso pode ser feito por meio de testes estatísticos apropriados e determinação do intervalo de confiança.
Interpretação cuidadosa dos resultados
É importante interpretar cuidadosamente os resultados, levando em consideração a significância estatística, o tamanho do efeito e outras considerações relevantes. A interpretação deve ser baseada em uma compreensão sólida dos métodos estatísticos usados.
Como a estatística pode ser usada para identificar tendências, prever resultados e fazer previsões?
Análise de séries temporais
A análise de séries temporais envolve a análise de dados que variam ao longo do tempo para identificar padrões e tendências. As técnicas de análise de séries temporais incluem a decomposição da série em seus componentes de tendência, sazonalidade e aleatoriedade, a fim de modelar e prever o comportamento futuro dos dados.
Modelos de regressão
A regressão é uma técnica estatística que relaciona uma variável de interesse com outras variáveis que podem influenciá-la. Os modelos de regressão podem ser usados para prever resultados futuros com base em variáveis independentes conhecidas. Por exemplo, um modelo de regressão pode ser usado para prever as vendas futuras de um produto com base no histórico de vendas, preço, publicidade e outros fatores que afetam as vendas.
Análise de tendências
A análise de tendências envolve a identificação de padrões e tendências em dados ao longo do tempo. As técnicas de análise de tendências incluem a análise de regressão, a análise de correlação e a análise de séries temporais. A análise de tendências pode ser usada para prever o comportamento futuro dos dados e fazer previsões.
Modelagem estatística
A modelagem estatística envolve a criação de modelos matemáticos para descrever e prever o comportamento dos dados. Esses modelos podem ser usados para prever o comportamento futuro dos dados com base em variáveis independentes conhecidas. A modelagem estatística é frequentemente usada em campos como finanças, marketing e ciência dos dados para prever tendências e fazer previsões.