O teste t de Student é uma ferramenta estatística indispensável para quem trabalha com análise de dados, melhoria de processos e validação de hipóteses. Criado para lidar com amostras pequenas e variabilidade desconhecida, o teste ganhou espaço em áreas como pesquisa científica, controle de qualidade, mercado financeiro e metodologias Lean.
Seja para comparar o desempenho de dois produtos, validar alterações de processos ou comprovar a efetividade de uma nova estratégia, o teste t ajuda a transformar observações em decisões embasadas. Neste artigo, você entenderá o que é o teste t de Student, como ele surgiu, quais são seus principais tipos, como calcular e interpretar os resultados e onde ele é mais aplicado — incluindo um exemplo prático na área industrial e sua integração em projetos Lean.
Se você busca fortalecer suas análises com métodos estatísticos confiáveis, siga na leitura.
O que é o teste t de Student?
O teste t de Student é uma ferramenta estatística usada para comparar médias e avaliar se duas amostras têm diferenças significativas. Desenvolvido para resolver problemas de análise com tamanhos de amostra pequenos, tornou-se fundamental em estudos científicos, pesquisas de mercado e controle de qualidade.
O método é baseado na distribuição t, que leva em conta a variabilidade dos dados e o tamanho da amostra. Quando a população tem variância desconhecida e o número de observações é limitado, o teste t oferece uma solução confiável. Dessa forma, permite tirar conclusões sobre uma população a partir de uma amostra, mesmo quando os dados são escassos.
Atualmente, o teste t de Student é amplamente utilizado na comparação de dois grupos, como, por exemplo, ao medir se um novo medicamento produz efeito diferente em relação a um placebo. Sua importância vai além da academia: está presente em ambientes corporativos, pesquisas clínicas e validações de processos industriais.
Sua origem
A história do nome "Student" chama atenção pela curiosidade que carrega. O teste foi criado por William Sealy Gosset, estatístico que trabalhava na cervejaria Guinness no início do século XX. Para manter o sigilo comercial e evitar que concorrentes soubessem que a empresa investia em métodos estatísticos, Gosset precisou publicar seus estudos sob um pseudônimo: "Student".
Em 1908, o artigo “The Probable Error of a Mean” foi publicado na revista Biometrika, introduzindo a distribuição t e o teste que hoje leva seu nome. Desde então, mesmo com o avanço de outras técnicas, o termo "teste t de Student" permaneceu. Ele é considerado um dos métodos mais confiáveis para trabalhar com amostras pequenas e variabilidade desconhecida.
Esse cuidado histórico ainda reforça a relevância do teste. Mesmo criado em circunstâncias específicas, seu impacto foi tão expressivo que transformou o modo como lidamos com dados até hoje.
Como calcular o teste t?
Fórmula geral:
O cálculo do teste t de Student é baseado na diferença entre as médias das amostras, ponderada pela variabilidade dos dados. A fórmula geral é expressa da seguinte forma:
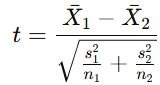
Onde:
- x̄1 e x̄2 são as médias das duas amostras.
- S1 e S2 são as variâncias das amostras.
- n1 e n2 representam os tamanhos das amostras.
Para o caso de teste t de uma única amostra, a fórmula é ligeiramente diferente:
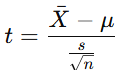
Nesse caso:
- μ é o valor esperado ou média populacional.
- s é o desvio padrão da amostra.
- n é o número de observações.
Etapas do cálculo passo a passo
Calcular o teste t de Student pode parecer técnico à primeira vista, mas o processo segue etapas bem definidas. Veja como fazer:
- Definir a hipótese nula e alternativa
Primeiro, é necessário estabelecer qual será a hipótese a ser testada. Em geral, a hipótese nula (H₀) propõe que não há diferença entre as médias. - Coletar a amostra e calcular as estatísticas básicas
Com os dados em mãos, calcula-se a média (Xˉ), o desvio padrão (s) e o número de elementos (n) para cada grupo. - Aplicar a fórmula correta
Usando as médias, desvios e tamanhos amostrais, substitui-se diretamente na fórmula correspondente ao tipo de teste (amostras independentes, pareadas ou única amostra). - Determinar os graus de liberdade (df)
O grau de liberdade varia conforme o teste:- Para duas amostras independentes: df=n1+n2−2
- Para uma amostra: df=n−1
- Comparar o valor calculado com o valor crítico da tabela t
Com o t calculado e o grau de liberdade, consulta-se a tabela t para o nível de significância definido (comum usar 5%). - Tomar a decisão
Se o valor de t calculado for maior que o valor crítico da tabela, rejeita-se a hipótese nula. Caso contrário, não se rejeita.
Principais tipos de teste t
Teste t para uma amostra
O teste t para uma amostra é utilizado quando se deseja comparar a média de uma amostra com um valor conhecido ou hipotético da população. Esse método avalia se a diferença observada é significativa ou se pode ter ocorrido apenas por variação aleatória.
Funciona bem em situações onde há um padrão pré-estabelecido. Imagine, por exemplo, uma fábrica que afirma que suas garrafas contêm exatamente 500 ml. Ao coletar uma amostra de garrafas e medir os volumes, o teste t permite verificar se a média da amostra realmente corresponde ao valor anunciado.
É importante lembrar que, nesse caso, a suposição é de que a população tem distribuição aproximadamente normal e que o desvio padrão populacional é desconhecido.
Representação gráfica: Um gráfico típico é o de uma distribuição t com uma linha vertical marcando a média da população e outra mostrando a média da amostra. A área sob a curva ilustra a região crítica (nível de significância).
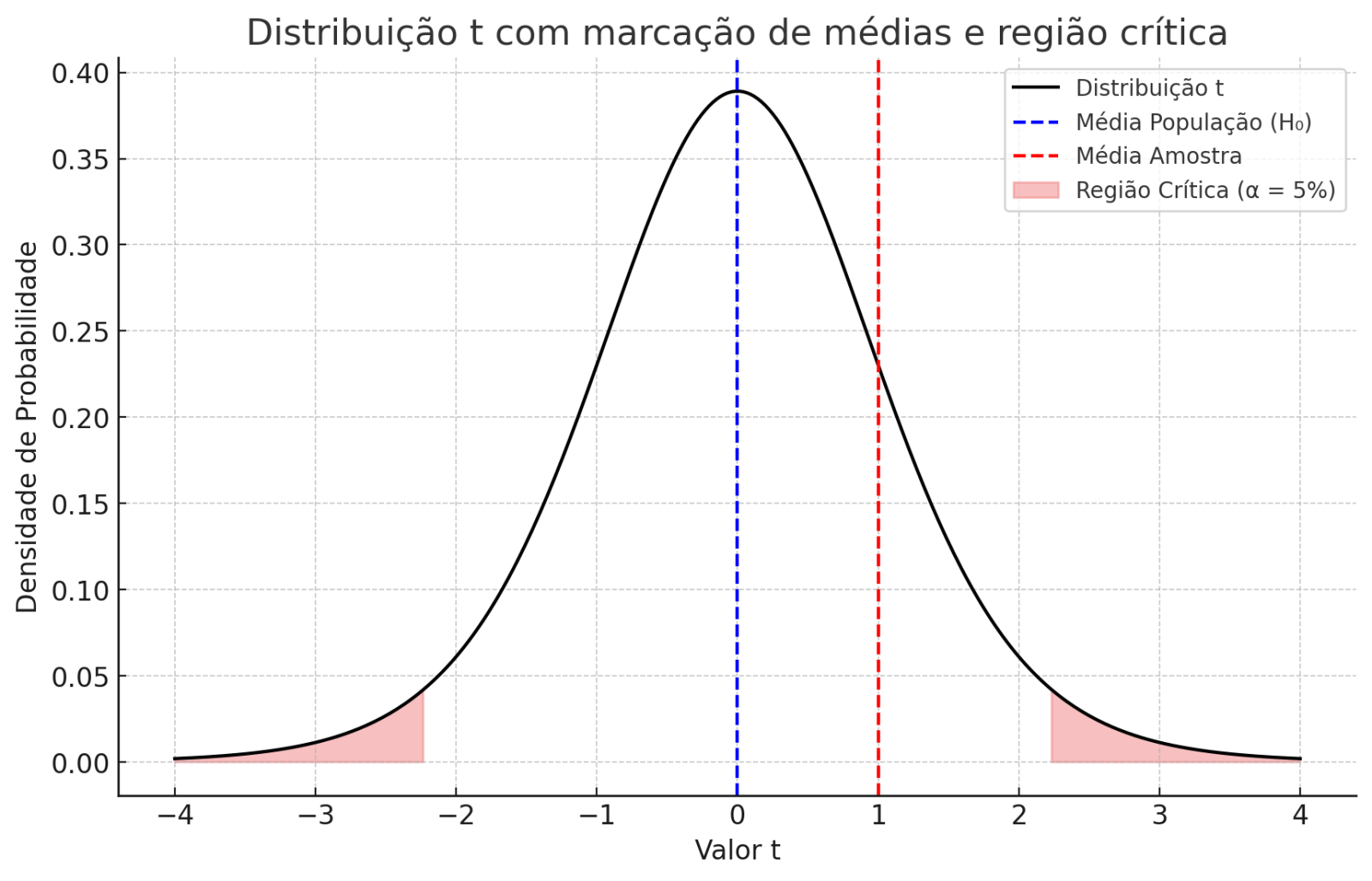
Teste t para amostras independentes
O teste t para amostras independentes compara as médias de dois grupos distintos, buscando identificar se há uma diferença significativa entre eles. É aplicado, por exemplo, ao comparar dois métodos de ensino usando alunos de turmas diferentes.
As amostras são independentes entre si, o que significa que a escolha ou resultado de um grupo não interfere no outro.
Representação gráfica:
Duas curvas de distribuição normal sobrepostas, cada uma representando um grupo. A separação entre as médias indica o tamanho do efeito.
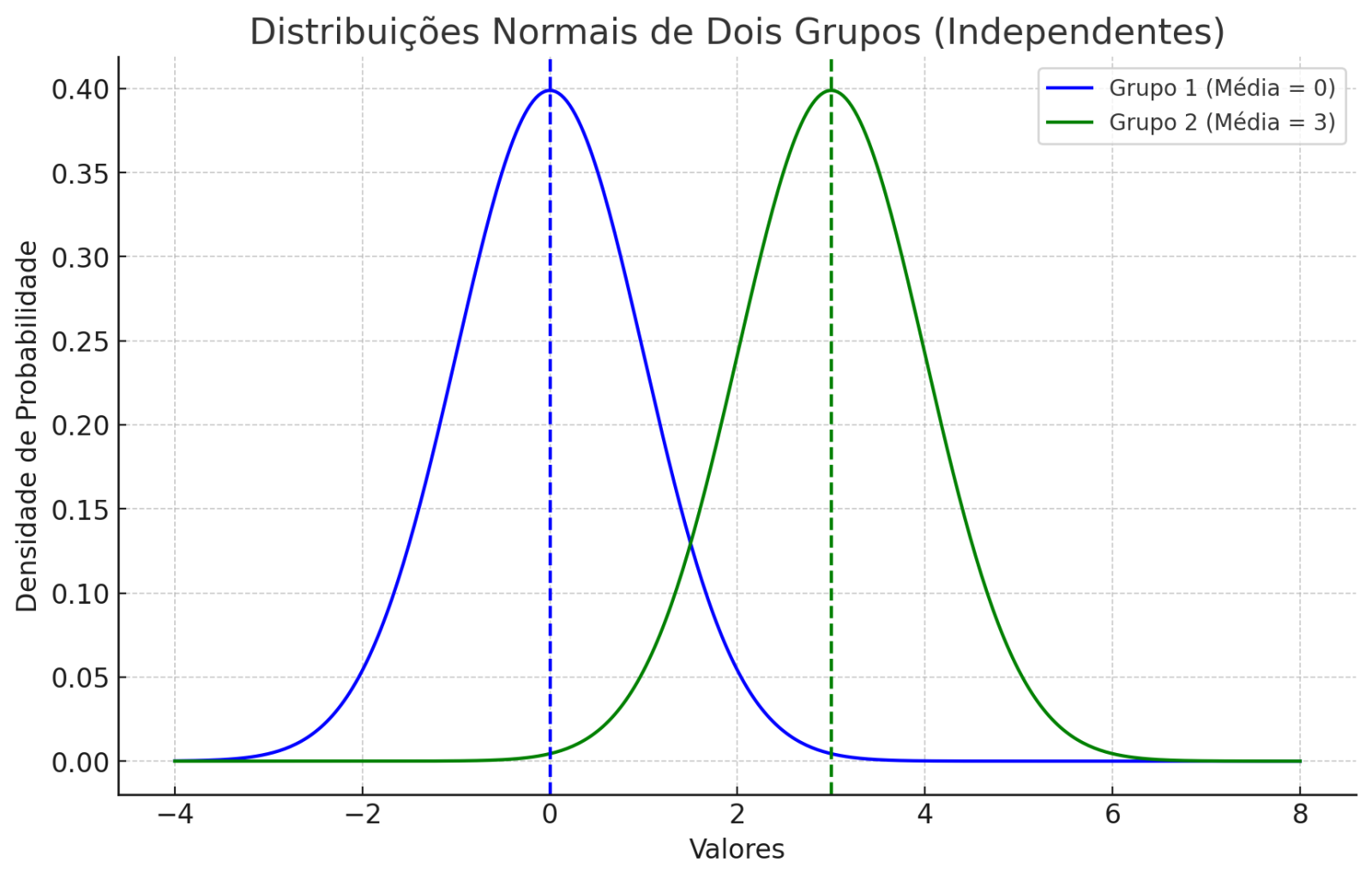
Teste t para amostras pareadas
O teste t para amostras pareadas é indicado para comparações em que cada indivíduo serve como seu próprio controle, como medições antes e depois de um treinamento.
Aqui, calcula-se a diferença entre os pares, e essas diferenças são analisadas como uma nova amostra.
Interpretação dos resultados
Valor de p (p-valor)
O p-valor é a medida que indica a probabilidade de observarmos um resultado tão extremo quanto o obtido, caso a hipótese nula seja verdadeira. Em testes estatísticos, ele é utilizado como critério para aceitar ou rejeitar a hipótese nula.
Quando se realiza um teste t de Student, o p-valor fornece o nível de evidência contra a hipótese de que não há diferença entre os grupos. Se o p-valor for menor do que o nível de significância adotado (geralmente 0,05), considera-se que o resultado é estatisticamente significativo.
De forma simples:
- p-valor < 0,05 → rejeita-se a hipótese nula (há diferença entre médias).
- p-valor ≥ 0,05 → não se rejeita a hipótese nula (não há evidência suficiente de diferença).
No contexto do teste t, interpretar corretamente o p-valor evita decisões precipitadas. É importante lembrar que um p-valor pequeno não mede a magnitude do efeito, apenas a força da evidência contra a hipótese nula.
Erro tipo I e erro tipo II
Toda decisão baseada em teste estatístico está sujeita a dois tipos de erros:
Erro Tipo I (α):
Ocorre quando se rejeita a hipótese nula mesmo ela sendo verdadeira. Em outras palavras, conclui-se que existe uma diferença entre médias quando, na realidade, não existe.
O nível de significância (α), que normalmente é 5%, representa a probabilidade máxima tolerada para cometer esse erro.
Erro Tipo II (β):
Acontece quando não se rejeita a hipótese nula mesmo ela sendo falsa. Ou seja, perde-se uma diferença real existente por falta de evidência estatística.
Esse erro está relacionado ao poder do teste (1 - β). Um poder baixo aumenta o risco de não detectar diferenças relevantes.
Exemplo: uso do teste t de Student na área de controle de qualidade
Imagine uma fábrica de parafusos que, para atender às normas técnicas, precisa garantir que o comprimento médio dos parafusos seja de 5,0 cm. Após uma manutenção no maquinário, o gestor de qualidade decide verificar se o novo ajuste alterou a produção.
Para isso, ele coleta uma amostra aleatória de 20 parafusos fabricados após a manutenção. O comprimento médio encontrado é de 5,1 cm, com um desvio padrão de 0,2 cm.
O gestor então aplica o teste t para uma amostra, comparando a média da nova produção com o valor de referência (5,0 cm).
Hipóteses estabelecidas:
- H₀ (hipótese nula): O comprimento médio dos parafusos continua sendo 5,0 cm.
- H₁ (hipótese alternativa): O comprimento médio dos parafusos é diferente de 5,0 cm.
Cálculo resumido:
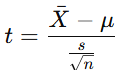
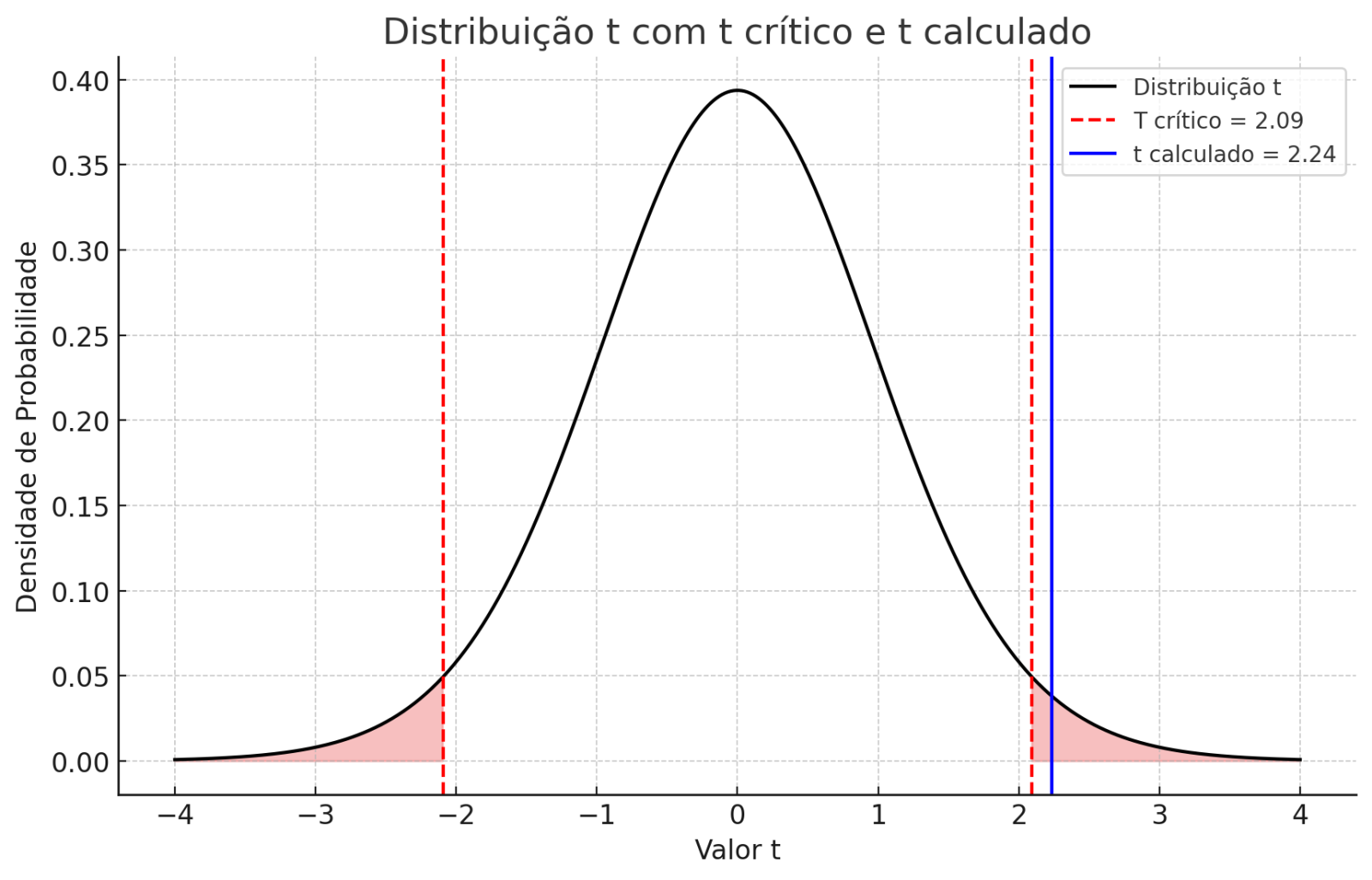
Aplica-se a fórmula do teste t para uma única amostra. Ao calcular o valor de t e comparar com o valor crítico da tabela t para 19 graus de liberdade e nível de 5% de significância, o gestor encontra que o t calculado não ultrapassa o valor crítico.
Definições importantes:
- t calculado: é o valor obtido a partir dos dados da amostra. Representa o quão distante a média da amostra está da média esperada, considerando a variabilidade dos dados.
- t crítico: é o valor de referência obtido na tabela da distribuição t para um determinado nível de significância (5%) e graus de liberdade (n-1 = 19). Neste caso, t crítico = 2,09.
Interpretação:
- Se o t calculado for maior que o t crítico, rejeitamos a hipótese nula.
- Como 2,24 > 2,09, rejeita-se a hipótese nula.
Conclusão: há evidência estatística para afirmar que o comprimento médio dos parafusos mudou após a manutenção da máquina. Ajustes no processo podem ser necessários para garantir a conformidade com o padrão.
Aplicação do teste t de Student no Lean
O teste t de Student é utilizado em projetos Lean, especialmente durante a fase de análise de dados em iniciativas de melhoria contínua. No contexto Lean, o objetivo é reduzir variações, eliminar desperdícios e garantir que alterações nos processos resultem em ganhos reais e sustentáveis.
Em projetos Lean Six Sigma, o teste t é empregado para validar hipóteses sobre mudanças em processos. Por exemplo, ao implementar uma nova padronização para reduzir o tempo de produção, é necessário verificar estatisticamente se o tempo médio realmente diminuiu após a mudança.
Nesse cenário, o teste t compara a média do processo antes e depois da implementação da melhoria, ajudando a comprovar se a diferença é significativa e não apenas fruto de variação aleatória.
Além disso, o teste t é essencial na verificação de estabilidade de processos (controle estatístico) e na validação de ganhos de produtividade, tempo de ciclo ou qualidade de produtos. Utilizar o teste corretamente evita conclusões precipitadas e garante decisões baseadas em dados sólidos.
Assim, integrar o teste t de Student em projetos Lean reforça a análise estatística das melhorias, apoiando ações de maneira mais segura e consistente.
Quer aprender como aplicar métodos estatísticos e projetos de melhoria contínua de forma prática? Inscreva-se gratuitamente no curso White Belt da FM2S e dê o primeiro passo para transformar dados em resultados.






