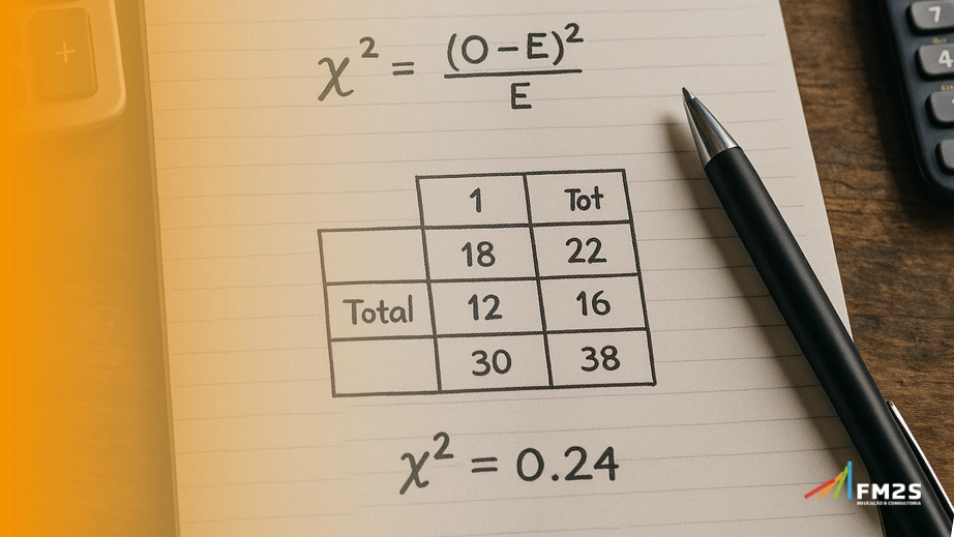Quando falamos em estatística, é comum focar na média, no desvio padrão ou no p-valor. Mas há um elemento que passa despercebido por muitos e que, silenciosamente, define a confiabilidade de boa parte dos testes, os graus de liberdade.
Esse conceito aparece em análises como o teste t de Student, ANOVA, qui-quadrado e até no cálculo da variância amostral. Apesar disso, nem sempre é compreendido com clareza. Na prática, ele representa quantas escolhas ainda podem ser feitas livremente em um conjunto de dados depois de aplicada uma restrição.
Se você lida com dados, cedo ou tarde vai precisar entender o papel dos graus de liberdade. Aqui, a ideia é deixar isso claro, sem rodeios.
O que são graus de liberdade na estatística?
Você já deve ter se deparado com o termo “graus de liberdade” ao estudar estatística, especialmente em testes como o t de Student ou na análise de variância (ANOVA). Mas o que, de fato, ele representa?
Graus de liberdade indicam quantos valores em um conjunto de dados podem variar livremente antes que alguma restrição matemática seja aplicada. Isso significa que, ao calcular certos parâmetros, como a variância, nem todos os dados da amostra podem mudar independentemente entre si. Existe uma limitação, geralmente imposta pelo uso da média amostral ou por outras condições definidas durante a análise.
Por exemplo, se você tem três números cuja média precisa ser 10. Você pode escolher os dois primeiros valores livremente, mas o terceiro já estará definido para garantir que a média seja mantida. Nesse exemplo, há dois graus de liberdade, ou seja, dois valores podem variar sem violar a condição da média.
Esse conceito é aplicado principalmente quando trabalhamos com estimativas. Sempre que usamos os próprios dados da amostra para calcular um parâmetro populacional, como a variância, é necessário ajustar o cálculo com base nos graus de liberdade disponíveis. Isso evita que a estimativa fique distorcida.
Como calcular os graus de liberdade no teste t de Student
O teste t de Student é uma ferramenta estatística usada para comparar médias. Mas, para que ele funcione, é preciso definir os graus de liberdade com base no tipo de teste e nas características da amostra.
Em termos simples, os graus de liberdade determinam o formato da distribuição t. Quanto menor o número de graus de liberdade, mais “espalhada” é a curva da distribuição. Isso impacta diretamente no valor crítico usado para avaliar a significância do teste.
Para uma amostra: teste t para média
Quando se trabalha com uma única amostra e o desvio padrão da população é desconhecido, os graus de liberdade são calculados da seguinte forma:
graus de liberdade (gl)= n −1
Onde n é o tamanho da amostra.
Isso ocorre porque, ao estimar a média amostral, um dos valores deixa de ser livre, ele fica preso à média. Essa perda de liberdade exige uma correção, e por isso usamos (n-1) no cálculo da estatística t.
Para duas amostras independentes
1. Com variâncias iguais (teste t padrão com variância agrupada):
gl = n₁ + n₂ - 2
Onde:
- n₁ é o número de observações da primeira amostra
- n₂ é o número de observações da segunda amostra
Esse modelo é mais simples e assume que as duas amostras vêm de populações com a mesma variância.
2. Com variâncias diferentes (Welch's t-test):
A fórmula aproximada dos graus de liberdade é:
gl = [ (s₁² / n₁) + (s₂² / n₂) ]² / [ ( (s₁² / n₁)² / (n₁ - 1) ) + ( (s₂² / n₂)² / (n₂ - 1) ) ]
Onde:
- s₁² = variância da primeira amostra
- s₂² = variância da segunda amostra
- n₁ = tamanho da primeira amostra
- n₂ = tamanho da segunda amostra
Esse método corrige os graus de liberdade levando em conta a diferença entre as variâncias. O resultado geralmente é um número decimal, que pode ser arredondado para baixo (em testes mais conservadores) ou deixado como está (dependendo do software).
Importância dos graus de liberdade em testes de hipótese
Em qualquer teste de hipótese, seja para comparar médias, proporções ou variâncias, os graus de liberdade estão no centro dos cálculos.
Quando o número de graus de liberdade é baixo, a distribuição t, F ou qui-quadrado se torna mais espalhada (com caudas mais largas). Isso significa que, para atingir o mesmo nível de significância (como 5%), o valor crítico necessário para rejeitar a hipótese nula será mais alto. Ou seja, a evidência observada precisa ser mais extrema para que o teste considere a diferença significativa.
Isso acontece porque, com menos dados disponíveis, há mais incerteza estatística. O teste se torna mais cauteloso, exigindo maior distância entre os valores observados e o que seria esperado sob a hipótese nula. Essa cautela reduz o risco de concluir algo que não está sustentado pelos dados mas, ao mesmo tempo, aumenta a chance de não detectar um efeito real (erro tipo II).
Entender essa relação evita interpretações equivocadas e melhora a leitura dos resultados em relatórios, estudos técnicos e decisões baseadas em dados.
O que são graus de liberdade na mecânica?
Na mecânica, o conceito de graus de liberdade descreve quantas maneiras independentes um corpo ou sistema pode se mover no espaço. A cada direção ou tipo de movimento possível representa um grau de liberdade.
Para entender melhor, pense em um ponto material, algo sem volume, como um ponto ideal em um plano. No espaço tridimensional, esse ponto pode se mover para frente e para trás (eixo x), para os lados (eixo y) e para cima e para baixo (eixo z). Isso dá três graus de liberdade translacionais.
Já um corpo rígido, como uma peça mecânica, pode também girar ao redor desses três eixos. Isso adiciona mais três graus de liberdade rotacionais, totalizando seis. Esse é o número máximo de movimentos independentes em um espaço tridimensional.
Quer aprender a resolver problemas com mais eficiência?
Comece pelo curso gratuito Yellow Belt da FM2S. Nele, você vai entender os fundamentos do Lean Seis Sigma e como aplicar ferramentas práticas de melhoria contínua no seu dia a dia.
É gratuito, online e com certificado.