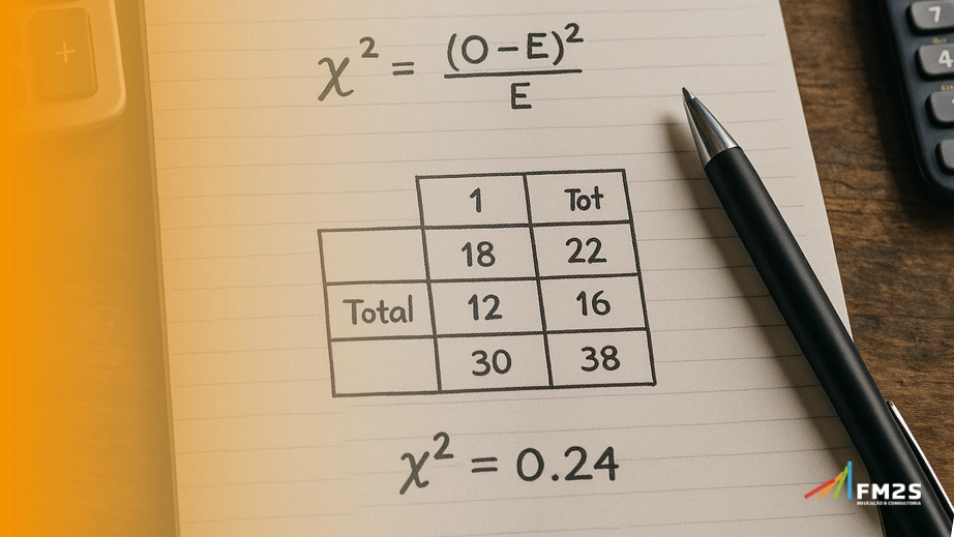Entender a relação entre variáveis é um passo essencial na análise de dados. No chão de fábrica, em uma pesquisa de opinião ou no controle de qualidade, identificar padrões e dependências ajuda a tomar decisões mais acertadas. É nesse cenário que o teste qui-quadrado ganha espaço: uma ferramenta estatística simples, mas eficiente, para lidar com variáveis categóricas.
Se você já se perguntou se a taxa de defeitos está associada ao turno de produção ou se o perfil de consumo muda conforme a região, o qui-quadrado pode trazer uma resposta baseada em evidência. Ao comparar frequências observadas com o que seria esperado por acaso, ele aponta se existe ou não uma associação entre os grupos analisados.
Ao longo deste conteúdo, você vai entender como o teste funciona, quando aplicá-lo, como interpretar os resultados e por que ele também pode ser útil em projetos Lean e de melhoria contínua.
O que é o teste qui-quadrado?
O teste qui-quadrado é uma ferramenta estatística usada para verificar se há associação entre variáveis categóricas. Em outras palavras, ele compara frequências observadas com frequências esperadas, partindo do pressuposto de que, na ausência de relação, as diferenças entre os valores seriam explicadas pelo acaso.
Esse teste é amplamente utilizado quando os dados são agrupados em tabelas de contingência. Por exemplo, ao analisar se o nível de satisfação de clientes depende da faixa etária, o qui-quadrado pode indicar se há relação entre as categorias analisadas ou se elas são independentes.
Vale destacar que o teste não mede a força da relação, apenas verifica se ela existe ou não com base na significância estatística. Por isso, é comum ver o qui-quadrado sendo aplicado em pesquisas eleitorais, testes de preferência de produto e estudos clínicos.
Quando aplicado corretamente, o teste qui-quadrado permite validar hipóteses de forma objetiva, principalmente quando os dados são classificados em categorias como "sim" ou "não", "alto", "médio" ou "baixo".
Importância no contexto de análise de dados
No ambiente de análise de dados, o teste qui-quadrado é utilizado para validar relações entre categorias sem exigir suposições fortes sobre distribuição dos dados. Isso o torna útil em contextos onde variáveis não são numéricas, mas ainda assim precisam ser comparadas de forma estatística.
Empresas utilizam o teste para entender se variáveis como “gênero” e “preferência por produto” estão associadas. Já na saúde pública, ele ajuda a verificar se há diferença significativa entre grupos de pacientes e tipos de tratamento. Em ambos os casos, a ferramenta permite tomar decisões baseadas em evidências e não em percepções isoladas.
Outro ponto relevante é a simplicidade do cálculo e a clareza da interpretação. Mesmo profissionais sem formação estatística avançada conseguem usar o teste, desde que observem suas limitações, como o tamanho mínimo da amostra e a necessidade de categorias mutuamente exclusivas.
Além disso, por ser amplamente aceito em publicações científicas, o qui-quadrado é uma escolha recorrente quando o objetivo é sustentar hipóteses com respaldo técnico. Ele conecta os dados brutos à inferência estatística, abrindo espaço para análises comparativas que impactam decisões operacionais, políticas ou acadêmicas.
Fórmula do teste qui-quadrado
A fórmula do teste qui-quadrado mede a diferença entre os valores que observamos na prática e aqueles que esperaríamos se não houvesse relação entre as variáveis. O cálculo parte de uma tabela de contingência, onde os dados são agrupados por categorias.
A equação básica é esta:
χ2=∑(O−E)^2/E (1)
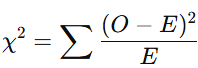
Onde:
- χ2: valor do qui-quadrado calculado
- O: frequência observada em cada célula da tabela
- E: frequência esperada em cada célula, assumindo independência entre as variáveis
- ∑: somatório de todas as células da tabela
A frequência esperada E é obtida multiplicando o total da linha pelo total da coluna e dividindo pelo total geral.
A fórmula resulta em um valor positivo. Quanto maior esse valor, maior a diferença entre os dados observados e o cenário de independência — o que pode indicar associação entre as variáveis.
Esse valor é comparado a um valor crítico de uma distribuição qui-quadrado, considerando os graus de liberdade e o nível de significância definido. Se o valor calculado ultrapassa o crítico, rejeita-se a hipótese de independência entre as variáveis.
Passo a passo com tabela de contingência
Para aplicar o teste qui-quadrado, é necessário organizar os dados em uma tabela de contingência, que distribui as frequências observadas entre duas variáveis categóricas. O processo exige atenção a cada etapa para garantir resultados confiáveis.
- Monte a tabela com as frequências observadas
Liste os dados reais obtidos na amostra. Cada célula representa o número de ocorrências combinadas entre as categorias das variáveis. Exemplo: número de pessoas satisfeitas ou insatisfeitas, por faixa etária.
- Calcule as frequências esperadas
Para cada célula, multiplique o total da linha pelo total da coluna e divida pelo total geral.
E=[(Total da linha)×(Total geral)]/E - Aplique a fórmula do qui-quadrado
Compare os valores observados (O) com os esperados (E), usando:
χ2=∑(O−E)^2/E
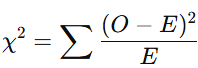
- Determine os graus de liberdade (GL)
Use a fórmula:
GL=(número de linhas−1)×(número de colunas−1) - Compare com o valor crítico ou calcule o valor de p
Com o resultado de χ2 e os graus de liberdade, consulte uma tabela estatística ou use software para verificar o valor de p.
Se o p for menor que o nível de significância (ex: 0,05), rejeita-se a hipótese de independência.
Esse passo a passo permite que o teste qui-quadrado seja aplicado de forma precisa, especialmente em análises que buscam identificar padrões entre grupos distintos.
Como interpretar os resultados?
Depois de calcular o valor do teste χ2, a interpretação dos resultados deve considerar:
- Valor de p (p-valor):
- Se p < 0,05 (nível de significância usual), rejeita-se a hipótese nula. Isso indica que há associação estatística entre as variáveis.
- Se p ≥ 0,05, não há evidência suficiente para rejeitar a hipótese nula. Nesse caso, presume-se que as variáveis são independentes.
- Graus de liberdade (GL):
- Calculados com:
GL=(número de linhas−1)×(número de colunas−1) - Eles determinam a distribuição teórica usada para comparar o valor de χ2.
- Calculados com:
- Frequências esperadas nas células:
- Devem ser iguais ou superiores a 5 em pelo menos 80% das células da tabela.
- Se esse critério não for atendido, os resultados do qui-quadrado podem ser distorcidos. Nesse caso, recomenda-se o teste exato de Fisher.
- Interpretação contextual:
- Um resultado significativo não implica em relação causal.
- A relevância prática deve ser analisada junto ao tamanho do efeito e ao contexto do estudo.
Esses cuidados ajudam a garantir que os resultados obtidos com o teste qui-quadrado sejam estatisticamente corretos e úteis para a tomada de decisão.
Quando usar o teste qui-quadrado?
O teste qui-quadrado é indicado quando se deseja verificar se há associação entre duas variáveis categóricas. Isso significa que ele é útil quando os dados são divididos em grupos, como "sim" e "não", "presente" e "ausente", ou faixas etárias, níveis de escolaridade, regiões geográficas, entre outros.
Esse teste pode ser aplicado em dois contextos principais:
- Para avaliar a independência entre variáveis em uma tabela de contingência. Por exemplo: existe relação entre o tipo de atendimento e o nível de satisfação dos clientes?
- Para verificar se as frequências observadas seguem uma distribuição teórica. Por exemplo: as proporções de escolha entre quatro sabores de um produto correspondem ao que foi projetado pela equipe de marketing?
É importante destacar que o qui-quadrado só deve ser usado quando:
- As variáveis forem categóricas, não contínuas.
- As frequências esperadas em cada célula forem iguais ou superiores a 5. Caso contrário, o teste perde confiabilidade.
- Os dados forem de uma amostra aleatória, com observações independentes entre si.
Quando os critérios são atendidos, o teste qui-quadrado se torna uma das formas mais diretas de identificar relações entre grupos em análises comparativas.
Exemplo: teste qui-quadrado aplicado à qualidade em uma fábrica de peças
Uma fábrica de peças automotivas quer verificar se existe relação entre o turno de produção (manhã, tarde e noite) e a ocorrência de defeitos.
Foram analisadas 300 peças, com a seguinte tabela de contingência (frequências observadas):
Turno | Peças com Defeito (O) | Peças Sem Defeito (O) | Total |
|---|---|---|---|
| Manhã | 20 | 80 | 100 |
| Tarde | 30 | 70 | 100 |
| Noite | 50 | 50 | 100 |
| Total | 100 | 200 | 300 |
Cálculo das frequências esperadas (E):
Para cada célula:
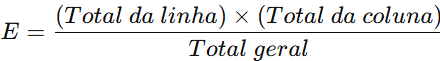
Exemplos:
- Manhã com defeito:
- E = (100 x 100) / 300 = 33,33
- Manhã sem defeito:
E = 66,67
Repetindo o cálculo para todas as combinações:
Turno | Peças com Defeito (E) | Peças Sem Defeito (E) | Total |
|---|---|---|---|
| Manhã | 33,33 | 66,67 | 100 |
| Tarde | 33,33 | 66,67 | 100 |
| Noite | 33,33 | 66,67 | 100 |
| Total | 100 | 200 | 300 |
Aplicando da fórmula (1):
Somando tudo:
χ2=5,33+2,67+0,33+0,17+8,33+4,17=21,00
Graus de liberdade (GL):
GL=(número de linhas−1)×(número de colunas−1) =
GL=(3−1)×(2−1)=2
Interpretação:
- Consultando a tabela qui-quadrado para GL = 2:
- Valor crítico para 5% de significância ≈ 5,99
- Como 21,00 > 5,99, rejeita-se a hipótese nula.
Existe evidência estatística de que o turno de produção influencia a ocorrência de defeitos. O turno da noite, com mais defeitos, deve ser investigado para ações corretivas.
Como aplicar o teste qui-quadrado no Lean?
Validação de melhorias no processo
No contexto do Lean Manufacturing, muitas ações de melhoria são implementadas para reduzir desperdícios, padronizar etapas e aumentar a eficiência. O teste qui-quadrado pode ser uma ferramenta útil para confirmar, com base estatística, se essas mudanças trouxeram efeitos reais.
Imagine que, após a aplicação do 5S em uma célula de trabalho, a equipe passou a registrar a quantidade de peças defeituosas por semana. Ao comparar as frequências de defeitos antes e depois da ação, o teste qui-quadrado pode indicar se houve mudança significativa ou se a variação observada é apenas aleatória.
Outro exemplo comum é a troca de layout. Suponha que, antes da mudança, 25% dos produtos apresentavam falha no acabamento. Após o novo arranjo físico, esse percentual caiu para 15%. O teste ajuda a avaliar se essa redução é estatisticamente significativa, e não apenas fruto do acaso.
Esse tipo de validação fortalece decisões dentro da rotina de melhoria contínua, pois vincula as ações Lean a evidências concretas, facilitando a priorização de novas intervenções.
Relação entre causas e defeitos (Análise de Causa Raiz)
Durante uma análise de causa raiz, especialmente quando se utiliza ferramentas como o Diagrama de Ishikawa ou o brainstorming estruturado, surgem diversas hipóteses sobre a origem de um defeito. O teste qui-quadrado permite verificar se há associação entre as possíveis causas e os tipos de falhas registrados.
Por exemplo, a fábrica pode observar que determinado tipo de defeito aparece com maior frequência no turno da noite. Ou que uma falha específica ocorre mais em uma máquina do que em outras. Organizando esses dados em uma tabela de contingência e aplicando o teste, é possível identificar se a frequência observada é realmente maior do que o esperado para aquela categoria.
Dessa forma, o qui-quadrado se torna um aliado na priorização de ações corretivas, ao distinguir padrões reais de variações aleatórias. Ele direciona o foco das investigações para os pontos mais críticos do processo, tornando a análise mais objetiva.
Quer aprofundar seus conhecimentos em melhoria de processos? Aprenda os princípios do Lean e descubra como aplicar métodos de análise para reduzir desperdícios e aumentar a eficiência com o curso gratuito Introdução ao Lean da FM2S.
.png)