Funções exponenciais são vastamente utilizadas na Matemática e em outras ciências correlacionadas com cálculos, como: Química, Biologia, Física, Engenharia, Astronomia, Economia e até mesmo Geografia. Na Matemática financeira, por exemplo, está associada ao crescimento de um capital aplicado a uma determinada taxa de juros compostos.
Outro fenômeno que é bastante estudado e que pode ser modelado por uma função exponencial é o decaimento radioativo, na Química. Na Geografia, pode ser usada em algumas situações para determinar o crescimento de algumas populações e, por fim, na Biologia apresenta-se como uma maneira de moldar o crescimento de bactérias em uma colônia, ou até mesmo o espalhamento de um vírus como o coronavírus, que será objeto do nosso estudo.
Funções Exponenciais
A função exponencial descreve situações em que uma quantidade cresce de forma proporcional ao seu valor atual. Esse tipo de comportamento é comum em fenômenos de propagação ou acumulação rápida.
Em outros casos de uso de crescimento (ou decrescimento) exponencial, esse número pode ser do tamanho de uma população animal ou do valor da sua conta bancária (se você tiver a sorte de ter boas taxas de juros).
Durante a pandemia, esse modelo ajudou a explicar a disseminação do coronavírus. No início da crise, a transmissão viral seguia uma função exponencial, pois cada pessoa infectada podia transmitir o vírus para várias outras, sem barreiras naturais ou imunológicas.
É por isso que epidemiologistas utilizam esse tipo de função para modelar surtos. Nos estágios iniciais, a curva de casos cresce rapidamente, um comportamento matematicamente previsível.
A Fórmula do Crescimento Exponencial
O crescimento exponencial é caracterizado pela seguinte fórmula:
X(t) = X0 . bt , onde:
- X(t) é o número de casos de coronavírus em qualquer instante de tempo “t”;
- X0 é o número de casos iniciais, também chamado de valor inicial;
- b é o número de pessoas infectadas por cada pessoa doente, também chamado de fator de crescimento;
- t é o tempo, que neste caso será medido em dias.
A fim de tornar nossa análise o mais verídica possível e tentarmos fazer estimativas mais reais, vamos olhar para os seguintes dados da doença:
- Uma pessoa infectada transmite o vírus para 2 a 3 pessoas em média;
- O tempo de incubação do vírus é em média de 5 a 6 dias, podendo chegar até 14 dias.
Obs.: Essas são apenas estipulações grosseiras a fim de contextualizar as funções exponenciais. Algumas matérias dizem que não necessariamente uma pessoa infectada irá transmitir o vírus para 2 ou 3 pessoas. Isso varia de ser humano para ser humano, da mesma forma que o tempo de incubação do vírus. O objetivo aqui é contextualizá-los a respeito deste tema quando um profissional da área da saúde cita a distribuição exponencial.
Simulação de Funções Exponenciais e o Coronavírus
Vamos agora fazer duas simulações para o caso do coronavírus. Vamos considerar primeiramente o cenário em que uma pessoa infectada consegue infectar outras 2 pessoas sadias, ou seja, b = 2. Para o segundo caso, vamos estipular que uma pessoa infectada consegue transmitir o vírus para outras 3 pessoas sadias. Quanto ao tempo em dias, vamos utilizar em ambos os casos (b=2 e b=3), os tempos “t” de 6 dias (caso mais real) e 14 dias (pior caso possível) de transmissão. Vamos conferir os cenários na tabela abaixo.
Em seguida, podemos usar esta fórmula para calcular o valor de y para cada valor de t. Quando fazemos isso, obtemos os números de pessoas infectadas a cada etapa do tempo, como visto na tabela. Isso mostra que a partir de 1 pessoa e com um fator de crescimento de b=2 por pessoa, obtemos mais de 16.000 casos após 14 dias. Para o caso em que b=3, após 14 dias obteremos mais de 4.700.000 casos. Preocupante, não acha?
Resolução passo a passo (cenários b=2 e b=3)
Usando a equação da função exponencial
X(t) = X₀ · bᵗ, com X₀ = 1 e t em dias.
Cenário 1: b = 2
- t = 6: X(6) = 1 · 2⁶ = 64
- t = 14: X(14) = 1 · 2¹⁴ = 16.384
Cenário 2: b = 3
- t = 6: X(6) = 1 · 3⁶ = 729
- t = 14: X(14) = 1 · 3¹⁴ = 4.782.969
Representando isso graficamente para os seis primeiros dias, começamos a ver um gráfico que se parece muito com as curvas muito alarmantes que vemos sobre o Coronavírus, porém em uma época de crescimento do número de casos.
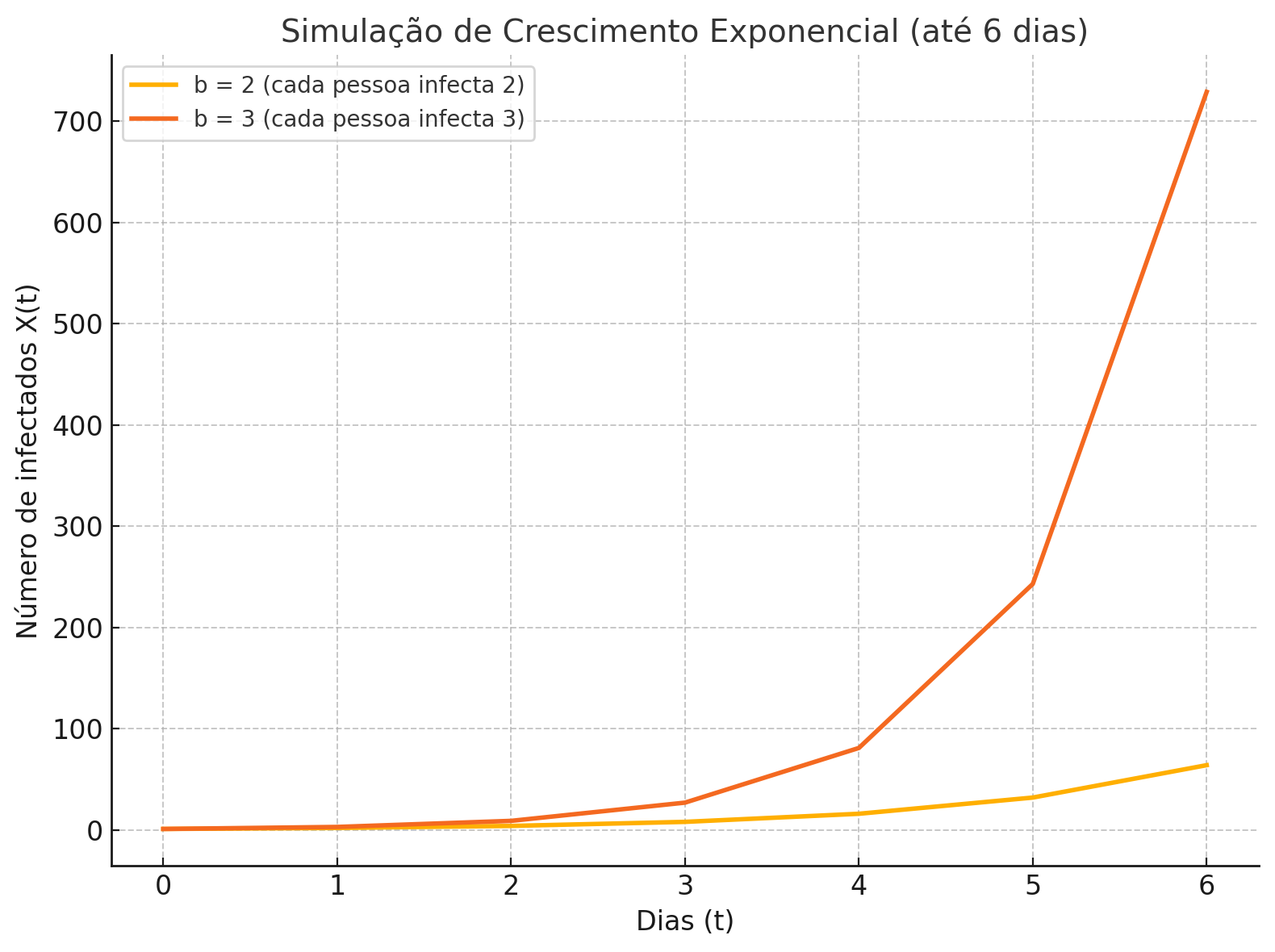
Uma observação importante é que utilizamos apenas os seis primeiros dias, pois se utilizássemos os 14 dias, a escala do gráfico não nos permitiria enxergar as curvas uma vez que 16.000 é um número extremamente menor que 4.700.000. Perceba que ambas as curvas têm o mesmo comportamento, com a diferença de que a curva de b=3 converge mais rápido que a curva de b=2.
Gráfico de Função Exponencial
O gráfico de uma função exponencial apresenta uma curva crescente que se eleva rapidamente. No início, os valores aumentam de forma lenta e quase imperceptível. Com o passar do tempo, a curva ganha inclinação e cresce de maneira acelerada, formando um traçado que sobe cada vez mais rápido à medida que o eixo do tempo avança.
Essa característica diferencia a função exponencial de uma função linear. Enquanto a linear cresce de forma constante, a exponencial tem um crescimento cada vez maior, resultado da multiplicação sucessiva dos valores.
Quando a base da função é maior que 1, o gráfico mostra crescimento exponencial. Já quando a base está entre 0 e 1, a curva aponta para baixo, representando um decaimento exponencial. Em ambos os casos, a curva nunca cruza o eixo X, mas se aproxima dele sem tocar, mostrando que os valores nunca chegam a zero.
Por que entender o crescimento exponencial é importante?
O comportamento de um surto viral pode ser comparado ao de uma função exponencial. À medida que o número de infectados aumenta rapidamente, cresce também a pressão sobre os sistemas de saúde. A necessidade de leitos hospitalares, equipamentos e profissionais pode se multiplicar em um curto espaço de tempo.
Durante a pandemia de COVID-19, esse efeito ficou evidente. Apesar da taxa de mortalidade relativamente baixa, a alta velocidade de transmissão levou a uma grande demanda por respiradores artificiais e internações simultâneas, o que sobrecarregou hospitais em diversos países.
Esse exemplo mostra como compreender o crescimento exponencial é essencial para planejar recursos e adotar medidas preventivas em situações de emergência. Reduzir o ritmo de contágio é a única forma de evitar o colapso de sistemas que não conseguem expandir sua capacidade na mesma velocidade da curva de casos.
Aprenda a analisar dados e tomar decisões melhores
Entender o comportamento exponencial é apenas um dos muitos exemplos de como a estatística pode apoiar decisões mais seguras e fundamentadas. Em empresas, hospitais e até na gestão pública, saber interpretar dados é o que permite prever cenários, alocar recursos de forma eficiente e evitar falhas críticas.
Se você deseja desenvolver essa habilidade, inscreva-se gratuitamente no curso Yellow Belt da FM2S. Nele, você aprende a aplicar conceitos estatísticos e ferramentas do Lean Six Sigma para resolver problemas , melhorar processos e destacar-se no mercado de trabalho.
.png)