Introdução
Muitas vezes não nos damos conta do quanto a estatística básica faz parte do nosso dia a dia. Ela está presente em praticamente tudo e nos permite realizar diversas análises e tirar importantes conclusões. A dispersão de uma doença ao longo do tempo seja ela por cidade, região ou faixa etária (como é o caso do novo coronavírus) é uma importante estatística a ser estudada, pois desta forma se tiram diversas conclusões sobre a propagação da doença como: número médio de pessoas que adquirem a doença no contato com uma pessoa doente, projeções de tempo para contaminação de uma grande população e muito mais.
Recomendamos também: Estatística descritiva básica e centralidade
Estatística Básica
Imagine a seguinte situação hipotética: você é um técnico de basquete e precisa escolher um dos jogadores do seu time para arremessar um lance livre que poderá trazer a vitória para o seu time. A questão é: qual jogador escolher para fazer o arremesso? A estatística é uma boa saída para esta questão, pois é ela que nos traz a média de pontos por jogo de cada jogador, chances de conversão em arremessos de três pontos, lances livres e por aí vai. Percebe a importância dessa análise para tomada de decisão?
O Lean Seis Sigma, por exemplo consiste em uma metodologia que utiliza da estatística para conferir qualidade a produtos/serviços e processos, além disso a estatística básica muito é requisitada pelos os Yellow, Green e Black Belts.
Aprofundando um pouco mais em um caso real da estatística aplicada ao Seis Sigma, vamos imaginar por exemplo uma máquina de corte de chapas de aço. A estatística de controle de qualidade, neste caso, é baseada no número de cortes corretos feitos pela máquina, cujos cortes com defeitos tendem a ser minimizados, adquirindo assim qualidade ao processo.
Uma vez contextualizados a respeito do que é a estatística básica e a sua importância no controle de qualidade e no processo de tomada de decisão, vamos nos aprofundar em alguns conceitos.
Estatística Básica – Variáveis
Variáveis estatísticas é o primeiro importante conceito que devemos observar. Consistem em incógnitas (por exemplo, o famoso X) que assume diferentes valores para diferentes elementos. São elas as responsáveis por lhe dar respostas para uma determinada situação que está sendo estudada. Vamos utilizar alguns exemplos para facilitar a compreensão:
- Qual é o número de pessoas entre 25 e 30 anos que adquiriram o novo coronavírus?
- Em qual faixa etária tem o maior número de mortes pela doença?
- Qual cidade possui o maior número de infectados?
Existe uma classificação que as variáveis podem assumir e elas se dividem entre variáveis qualitativas e quantitativas.
Variáveis quantitativas, são variáveis que assumem valores numéricos e podem ser discretas ou contínuas. As variáveis discretas assumem apenas valores inteiros e contáveis, por exemplo, o número de nascimentos em um hospital ao longo de um ano. Perceba que essa informação não pode assumir um valor decimal como 130,8 e sim apenas um valor fixo inteiro como 130 ou 131. Já as variáveis contínuas são as que podem assumir quaisquer valores, seja ele um valor “quebrado”, inteiro ou até mesmo negativo.
Variáveis qualitativas descrevem exatamente tudo aquilo que não pode assumir um valor numérico, mas que se classificam e categorias e se dividem entre qualitativas nominais e ordinais. As variáveis qualitativas ordinais descrevem uma ordem entre as categorias como por exemplo o grau de escolaridade, o tamanho de uma peça de roupa ou uma classe social. Já as variáveis de qualidade nominais não há ordenação entre categorias e geralmente são aleatórias, como no caso de um atendimento médico, o bairro ou região onde o paciente reside.
População e Amostra
População é conhecida como o alvo de um estudo. Consiste no total de elementos (pessoas ou objetos) que estão englobados nas características do estudo em questão. Por exemplo queremos saber a altura média das pessoas na cidade de São Paulo, logo pessoas em geral fazem parte da nossa população. Já a amostra, corresponde a uma parte da população que é utilizada para um estudo, neste caso, pessoas que vivem na cidade de São Paulo, fazem parte de uma amostra.
Aqui entra uma questão interessante e muito discutida entre os especialistas da área, que é o tamanho da amostra. Quanto maior for a sua amostra, maior a confiabilidade dos seus dados. Você deve concordar que se estivermos buscando a altura média das pessoas na cidade de São Paulo e pegarmos uma amostra de dez pessoas, fica difícil estimar isto, uma vez que ao acaso, você pode ter pego dez pessoas muito altas ou muito baixas, fazendo com que o seu estudo perca o nível de confiança e aumente a margem de erro, concorda?
Quando a amostra não representa corretamente a população, diz-se enviesada, ou seja, esta amostra pode dar margem a interpretações e conclusões erradas a respeito de uma população. Pensando no caso de uma doença, isso pode ser crítico, da mesma forma que para um produto de uma empresa, acarretando em sua falência. Desta forma, vamos conferir os diferentes métodos para dimensionamento de amostras. Em sua maioria são compostos por cálculos simples que com o auxílio de uma calculadora é possível determinar.
Dimensionamento de Amostra
Dimensionar o tamanho ideal de uma amostra é fundamental para conseguirmos ter um retrato fiel de uma população uma vez que amostras muito pequenas podem induzir a erros e amostras excessivamente grandes podem ser um grande desperdício de tempo e de dinheiro.
Sabendo o que é uma amostra e os problemas que podemos enfrentar caso esta não seja um retrato fiel da população objeto do nosso estudo, vamos conferir alguns métodos para dimensionar seu tamanho.
Tamanho de Amostra com base na Média Aritmética
Vamos supor que estejamos interessados em estimar a renda média das pessoas que concluíram um curso de Especialista Lean na FM2S, um ano após a conclusão do mesmo. Desta forma eu lhe pergunto: Quantas rendas devem ser incluídas em nossa amostra? Uma das forma de se dimensionar uma amostra é com base na renda média populacional através da fórmula:
n = [(Z α/2.σ)/d]²
Onde:
n = Número de indivíduos na amostra;
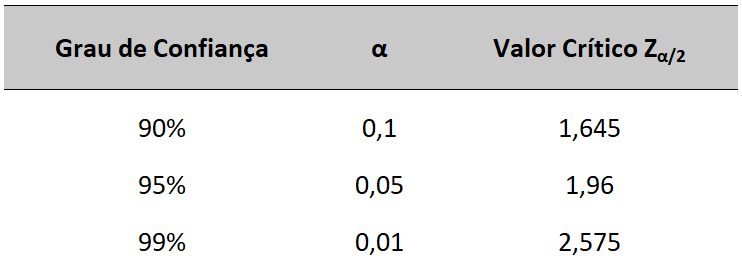
Z α/2 = Valor crítico que corresponde ao grau de confiança desejado;
σ = Desvio padrão da variável populacional estudada (neste caso a renda);
d = Margem de erro ou erro máximo da estimativa (consiste no valor da diferença entre a média amostral () e a média populacional).
Os valores de confiança mais utilizados e os valores de Z são tabelados conforme mostrado abaixo.
 Tamanho da Amostra com base na estimativa da proporção populacional
Tamanho da Amostra com base na estimativa da proporção populacional
Eis um outro parâmetro que afeta o tamanho da amostra: a proporção populacional. Para isso vamos pensar na proporção de pessoas atendidas por uma unidade de saúde. Assim a fórmula para o tamanho da amostra fica:
n = (z².p.q)/d²
Onde:
n = Número de indivíduos na amostra;
Z α/2 = Valor crítico que corresponde ao grau de confiança desejado;
σ = Desvio padrão da variável populacional estudada (neste caso a renda);
p = Proporção de indivíduos que pertencem a categoria de interesse do nosso estudo;
q = Proporção de indivíduos que não pertencem a categoria de interesse (q = 1 - p);
d = Margem de erro ou erro máximo da estimativa (consiste no valor da diferença entre a média amostral e a média populacional).
Obs: caso os valores de p e q não sejam conhecidos, o recomendado é utilizar 0,5 para cada um deles.
Tamanho da amostra para populações finitas
Todas as formas de estimar as amostras que vimos até aqui, partem do pressuposto de que a população é tão grande que pode ser considerada infinita. No entanto, caso a amostra “n” tenha um tamanho maior ou igual a 5% da população “N” considera-se uma população finita e assim, adiciona-se um fator de correção nas fórmulas que vimos anteriormente, assim ficamos com: Fórmula para determinação do tamanho da amostra (n) com base na estimativa da média populacional:
n = {(Z²α/2.σ².N)/[d².(N-1)+ Z²α/2.σ²]}
Determinação do tamanho da amostra (n) com base na estimativa da proporção populacional:
n = {( Z²α/2. σ².N)/[d².(N-1)+ Z²α/2².p.q]}
Amostragem em Lean Seis Sigma
A amostragem na metodologia Lean Seis Sigma é dada em geral na fase Measure do roteiro DMAIC, o roteiro responsável por guiar a metodologia. As fontes de dados desta fase do DMAIC, geralmente são obtidas primeiramente através de reuniões com os colaboradores, regerando na maioria dos casos dados qualitativos. Em segundo lugar, responsável pela coleta quantitativa, é realizado o processo de amostragem. O processo quantitativo pode se iniciar com a quantidade de produtos produzidos. Para os casos em que a quantidade é um fator insignificante do processo de melhoria, a amostra é considerada infinita.
A partir de então inicia-se o processo de determinação do tamanho da amostra. Para o exemplo de uma linha de produção de um produto, pode-se utilizar a estimativa da proporção populacional, já que é considerado o valor da proporção estimada. A proporção é baseada em experiências passadas ou em uma amostra piloto.
Na seleção da amostra piloto pode-se considerar uma amostragem probabilística com o intuito de realizar a coleta de forma aleatória e sem interferência do pesquisador. A amostragem pode ser realizada em seis subgrupos possuindo um tempo pré-estabelecido, sem aviso prévio de dia e horário, a fim de garantir uma aleatoriedade.
Conclusão
Com o término da amostragem piloto obtemos a proporção dos itens defeituosos, ou seja, produtos fora dos limites de especificação e, a partir disso, identificou-se o tamanho real da amostra que iria representar a população. Este é um exemplo de como a estatística básica se aplica ao Seis Sigma.
Assim, os dados são tratados e colocados em gráficos de controle e dispersão, histogramas e muitas outras ferramentas da qualidade. Você pode encontrar diversas ferramentas da qualidade em nosso material de apoio.
Existem programas específicos para tratamento desses dados, até mesmo em tempo real. O Power BI é uma ferramenta especializada em realizar esse tipo de tratamento que consegue atualização de informações em tempo real. Aproveite para conhecer nossa formação em visualização de dados e aprender como elaborar bons dashboards.
Não deixe de conhecer a certificação Lean Seis Sigma em nossa Plataforma EAD. Pra você que está inciando agora, conheça o nosso curso White Belt gratuito.