O Desvio Padrão consiste em uma medida do nível de dispersão, isto é, ele indica quão uniforme está um conjunto de dados. Ou seja, quanto maior o Desv. Padrão, o conjunto de dados está mais distante da média.
Quanto mais próximo de 0 ele estiver, temos o desvio padrão mais homogêneo. Confira no detalhe o que é Desvio Padrão neste artigo.
O que significa um desvio padrão?
O desvio padrão é uma medida de dispersão ou variabilidade em estatísticas e probabilidade. Ele indica o grau de variação ou dispersão dos dados em um conjunto em relação à média (valor médio) desse conjunto. Em outras palavras, o desvio padrão ajuda a entender o quão distantes os valores individuais estão da média.
Um desvio padrão baixo sugere que a maioria dos dados está concentrada em torno da média, enquanto um desvio padrão alto indica que os dados estão mais espalhados. O desvio padrão é frequentemente utilizado para identificar padrões, anomalias ou outliers em conjuntos de dados e para entender a incerteza ou precisão das estimativas estatísticas.
O desvio padrão é calculado como a raiz quadrada da variância, que é a média dos quadrados das diferenças entre cada valor e a média do conjunto de dados.
O Green Belt é a certificação mais conhecida do Lean Six Sigma. Nela, são abordados conceitos fundamentais para otimização de processos e resultados nas empresas. Essa certificação torna o aluno apto a transformar uma grande quantidade de dados em informações valiosas para a tomada de decisão e a analisar criticamente os processos, eliminando desperdícios, desconexões e problemas crônicos entre eles.

Como fazer o cálculo de desvio padrão?
O desvio padrão é uma medida de dispersão de um conjunto de dados, ou seja, um coeficiente de variação desses dados. É comum, estarmos interessados no desvio padrão de uma população, por exemplo. No entanto, utilizamos dados de uma amostra para estimar o desvio de uma população a partir do desvio dessa amostra.
Por exemplo, no caso de uma biblioteca de escola: quantos livros eles alugaram no último mês? Assim temos toda a população escolar envolvida, pois a pergunta se dirige a todos os alunos .
Em tais casos, utiliza-se o desvio da população. No entanto, às vezes não é possível encontrar informações sobre uma população inteira e pode ser mais fácil usar uma amostra de 150 alunos para estimar dados sobre toda a população escolar.
A partir disso, usamos esses resultados para determinar os hábitos de empréstimo da biblioteca para toda a população de estudantes. Nestes casos, utiliza-se o desvio da amostra.
Qual a fórmula do Desvio Padrão?
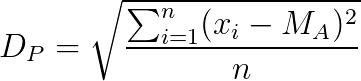
Onde:
Dp: é o desvio; Xi: é um valor qualquer no conjunto de dados na posição i; MA: É a média aritmética do conjunto dos dados; n: é a quantidade total dos dados no conjunto.
Exemplo de desvio padrão
Exemplo: Em uma equipe de basquete, os atletas possuem as seguintes alturas: 1,80; 1,95; 1,98; 1,88; 2,04. Qual a altura média da equipe? E qual o desvio padrão de altura da equipe?
Primeiramente, calculando a média, temos:
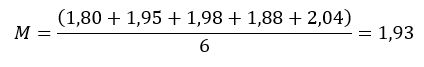
Em seguida, calculando o desvio padrão, temos:
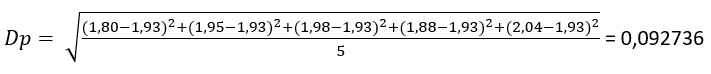
Como interpretar o valor do desvio padrão?
Interpretar o valor do desvio padrão envolve entender como os dados estão dispersos em relação à média do conjunto de dados. A seguir estão algumas orientações para ajudar na interpretação do desvio padrão:
- Desvio padrão igual a zero: isso significa que todos os valores do conjunto de dados são iguais à média e não há variação. Os dados são perfeitamente uniformes;
- Desvio padrão baixo: um desvio padrão baixo indica que a maioria dos valores do conjunto de dados está próxima da média. Os dados são menos dispersos e estão concentrados em torno da média;
- Desvio padrão alto: um desvio padrão alto sugere que os valores estão mais distantes da média e há uma maior dispersão dos dados.
Para uma interpretação mais concreta, é possível utilizar a regra empírica de 68-95-99,7, que é válida para conjuntos de dados com distribuição normal (ou aproximadamente normal):
- 68% dos valores do conjunto de dados estão dentro de 1 desvio padrão da média (média ± 1 desvio padrão);
- 95% dos valores do conjunto de dados estão dentro de 2 desvios padrão da média (média ± 2 desvios padrão);
- 99,7% dos valores do conjunto de dados estão dentro de 3 desvios padrão da média (média ± 3 desvios padrão).
Lembre-se de que a aplicabilidade dessa regra depende da distribuição dos dados. Se os dados não seguirem uma distribuição normal, a regra pode não se aplicar diretamente.
Em geral, o desvio padrão é uma ferramenta útil para compreender a dispersão dos dados, identificar outliers e avaliar a precisão de estimativas estatísticas.
Variância e Desvio Padrão
A variância, bem como o desvio também é uma medida de dispersão que indica a regularidade de um conjunto de dados em torno da média. Ela é semelhante ao próprio desvio padrão uma vez que um deriva-se do outro.
A variância é calculada como o quadrado do desvio padrão, que resulta basicamente na exclusão da raiz quadrada da fórmula do desv. padrão, assim a variância é dada por:
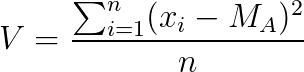
Qual a fórmula do desvio padrão no Excel? (Passo a passo)
Uma ferramenta bastante utilizada nos cálculos estatísticos é o Microsoft Excel, logo vamos ensinar agora como calcular o desvio padrão de uma amostra utilizando o software.
Para tal, empregaremos o exemplo da equipe de basquete mencionado anteriormente.
1º Passo: Disponha seus dados em uma mesma coluna
Antes de iniciar o cálculo, é necessário dispor os dados a serem trabalhados em uma mesma coluna, como na imagem abaixo.
2º Passo: Inserir a fórmula do desvio padrão (DESVPAD.P)
Para inserir quaisquer fórmulas no Excel, antes de tudo você deve colocar o sinal de igual "=".
Em seguida, você deve digitar a função DESVPAD.P e assim, selecionar o intervalo onde os argumentos da função estão contidos.
Passo 3: Por fim, basta apertar a tecla "Enter" ou "Return" que o resultado irá aparecer na célula onde a fórmula foi inserida.
Na metodologia seis sigma o desvio padrão é bastante utilizado para moldar distribuições de probabilidade.
Como por exemplo a distribuição normal, muito característica desta metodologia e conhecida como a mais importante distribuição de probabilidade.
Quando usar o desvio padrão da amostra ou da população?
Na maioria das vezes, estamos interessados em saber o desvio padrão de uma população, ou seja, de uma quantidade muito grande de dados.
Isso porque a população é o nosso objeto de interesse. Portanto, você normalmente calcularia desvio da população se:
- Você tiver toda a população ou;
- Você tiver uma amostra de uma população maior, mas você só está interessado nesta amostra e não deseja generalizar suas descobertas para a população.
No entanto, em estatística, geralmente utiliza-se com uma amostra da qual desejamos estimar (generalizar para) uma população, e o desvio padrão não é uma exceção para isso.
Portanto, se tudo o que você tem é uma amostra, mas deseja uma declaração sobre o desvio da população a partir da amostra, você usa o desvio padrão da amostra. Por exemplo, para calcular a média de altura das crianças de um colégio de 1000 alunos (população) você não precisa medir a altura de todos.
Você pega uma amostra da população, ou seja, 100 alunos e a partir disso estima a altura média. Porém um problema pode acontecer e é preciso estar atento no caso de você pegar essa amostra com 100 alunos muito baixos, ou muito altos o que não seria uma boa representação da sua população.
A sacada aqui é estimar um tamanho de amostra que represente de fato a sua população.
Qual a importância de saber o desvio padrão?
Saber o desvio padrão é importante por várias razões, especialmente em estatísticas, pesquisa e análise de dados. Algumas das principais aplicações e importância do desvio padrão incluem:
- Medir a dispersão dos dados: fornece informações sobre o grau de dispersão dos dados em um conjunto. Compreender a dispersão é crucial para a análise de dados, pois ajuda a identificar se os dados estão concentrados em torno da média ou espalhados ao longo de um intervalo mais amplo;
- Identificar outliers: pode ser usado para detectar valores extremos ou outliers em um conjunto de dados. Valores que estão muito distantes da média (por exemplo, mais de 2 ou 3 desvios padrão) podem ser considerados outliers e merecem investigação adicional;
- Comparação de conjuntos de dados: permite comparar a variabilidade entre diferentes conjuntos de dados, mesmo que eles tenham médias diferentes. Isso é útil, por exemplo, na comparação do desempenho de diferentes investimentos, processos de fabricação ou resultados de pesquisas científicas;
- Avaliar a precisão de estimativas: o desvio padrão é frequentemente usado para quantificar a incerteza ou a precisão das estimativas estatísticas, como médias e proporções. Um desvio padrão menor indica que as estimativas são mais precisas e têm menos variabilidade;
- Distribuição normal e regra empírica: em conjuntos de dados com distribuição normal, o desvio padrão ajuda a aplicar a regra empírica de 68-95-99,7 para entender a proporção de dados que caem dentro de intervalos específicos em torno da média;
- Controle de qualidade: em processos industriais, o desvio padrão é usado no controle estatístico de qualidade para monitorar e melhorar a consistência e a qualidade dos produtos.
Saber o desvio padrão é fundamental para tomar decisões informadas, interpretar resultados e compreender a variabilidade em várias áreas, como finanças, ciência, engenharia e pesquisa.
Quais os tipos de desvios padrões?
As variações de causa comuns são os fatores sempre presentes (ou seja, entradas ou condições do processo) que contribuem em vários graus para mudanças relativamente pequenas, ou seja, aparecem ser aleatórias, em resultados dia após dia, semana após semana.
Esses fatores atuam de forma bem independente uns dos outros. O efeito coletivo de todas as causas comuns referem-se, muitas vezes como variação do sistema porque define a quantidade de variação inerente ao sistema.
Geralmente é difícil, se não impossível, vincular variação de causa aleatória e comum a qualquer fonte particular. Estes podem incluir variação composta induzida pelo ruído, vibração operacional e eficiência da máquina e geralmente são difíceis de identificar e avaliar porque são de natureza aleatória.
No entanto, se apenas a variação aleatória estiver presente, a saída do processo forma uma distribuição estável ao longo do tempo.
As variações de causas especiais são fatores que induzem disparidades, além de variações aleatórias. Frequentemente, a variação da causa especial aparece como um efeito extremo ou algum padrão específico e identificável nos dados.
As causas especiais referem-se, muitas vezes, como causas atribuíveis porque a variação produzida é rastreada e atribuída a uma fonte identificável. Estes incluem variações induzidas por efeitos especiais nem sempre presentes ou incorporados ao processo.
Visto que, alguns exemplos incluem: temperatura induzida e fatores ambientais não controlados, sobretensões, pessoas, mudanças no processo, ajustes de ferramentas, erro de medição e variações de material.






