O gráfico de dispersão é uma ferramenta gráfica amplamente utilizada em estatística e outras áreas do conhecimento para visualizar a relação entre duas variáveis quantitativas. Ao plotar os pontos no gráfico, é possível detectar padrões e tendências nos dados e identificar possíveis correlações entre as variáveis.
Essa visualização pode fornecer insights importantes para análise de dados e tomada de decisão em diversas áreas, desde a pesquisa de mercado até a análise de dados científicos.
Neste artigo, vamos explorar em detalhes o que é um gráfico de dispersão, como interpretar seus resultados e como aplicá-lo em diferentes contextos.
O que é e para que serve o Gráfico de Dispersão?
Dispersão é um conceito estatístico que se refere à variabilidade dos dados em torno de uma medida central, como a média. Em outras palavras, a dispersão indica o quão "espalhados" ou variados são os valores de uma amostra ou população. É uma medida importante, pois permite avaliar a consistência dos dados e identificar possíveis padrões ou outliers.
Existem várias medidas de dispersão, sendo as mais comuns a variância e o desvio padrão. A variância é uma medida de quão longe os valores estão da média, enquanto o desvio padrão é a raiz quadrada da variância e é uma medida mais comumente utilizada por ser expressa na mesma unidade dos dados originais. Outras medidas de dispersão incluem o desvio absoluto médio, a amplitude e o intervalo interquartil.
Quais são as principais medidas de dispersão?
Variância
É uma medida que indica a média dos desvios quadrados dos dados em relação à média. A variância é calculada pela soma dos desvios quadrados dividida pelo número de dados menos um.
Desvio padrão
É a raiz quadrada da variância e indica o quão dispersos os dados estão em relação à média. É uma medida mais comumente utilizada por ser expressa na mesma unidade dos dados originais.
O que é o Gráfico de Dispersão ou Scatterplot?
O gráfico de dispersão é um tipo de gráfico utilizado para representar a relação entre duas variáveis quantitativas. Ele é construído plotando os valores de uma variável no eixo horizontal e os valores da outra variável no eixo vertical. Cada par de valores é representado por um ponto no gráfico.
O objetivo do gráfico de dispersão é permitir que se visualize a relação entre as duas variáveis. Dependendo do padrão observado, é possível identificar diferentes tipos de relação entre as variáveis, como uma relação linear, uma relação não linear, uma relação positiva ou negativa, entre outras.
Além disso, o gráfico de dispersão também pode ser utilizado para identificar valores discrepantes (outliers) e avaliar a consistência dos dados. É uma ferramenta gráfica muito útil em diversas áreas do conhecimento, como a estatística, a física, a biologia, a ecologia e a economia, entre outras.
Exemplo de gráfico de dispersão
Vamos ilustrar melhor: por exemplo, no caso do departamento de gerenciamento de projetos que esta interessado em aumentar a satisfação com relação à entrega dos projetos, coletamos os dados de satisfação (através de um formulário com o cliente) e de atraso (atraso negativo significa que o projeto foi entregue antes do prazo). Os dados são anotados em pares (x, y)..
Lembre-se: o primeiro passo para se traçar um bom gráfico de dispersão, é coletar bons dados.
Tabela 1 - Dados sobre atraso e satisfação para vários projetos.
| Projeto | Dias de atraso | Satisfação |
| 1 | -3 | 3.90 |
| 2 | -6 | 3.42 |
| 3 | -1 | 3.10 |
| 4 | 0 | 2.95 |
| 5 | 4 | 1.83 |
| 6 | 5 | 2.25 |
| 7 | 9 | 1.92 |
| 8 | 11 | 3.15 |
| 9 | 19 | 2.85 |
| 10 | 12 | 3.00 |
| 11 | -5 | 2.64 |
| 12 | -6 | 3.96 |
| ... | ... | .... |
Após coletarmos os dados, podemos usar um software para nos auxiliar a traçar o gráfico de dispersão. Um que gostamos bastante é o Minitab. Ele não só nos ajuda a traçar o gráfico, mas também tem alguns recursos adicionais que nos ajudam a entender correlações e estratificações de dados.

Entretanto, quem prefere o Excel, pode facilmente encontrar várias opções de gráfico de dispersão nele. Algumas das opções até colocam linhas de regressão linear, considerada uma sofisticação do gráfico.
No exemplo, usamos o Minitab e obtemos o seguinte gráfico:
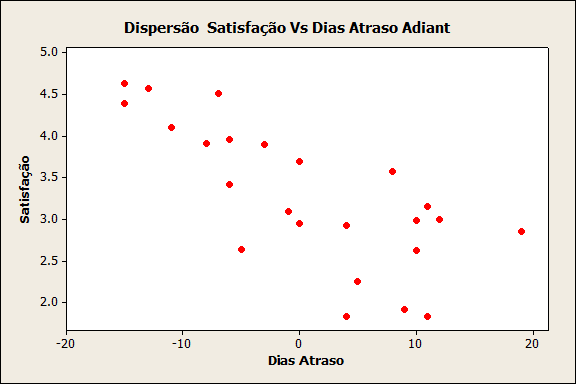
Quais são as possíveis correlações a serem identificadas em um gráfico de dispersão?
Além da correlação negativa forte, podemos ter as seguintes correlações entre duas variáveis (que são identificadas usando-se o gráfico de dispersão).
- Sem correlação: quando vemos apenas uma nuvem de pontos no gráfico, podemos dizer que não há correlação entre a variável Y e a variável X. Os seus valores não estão de maneira alguma atrelados;
- Correlação positiva forte: há uma clara tendência nos dados. Quando a variável X aumenta, é esperado conjuntamente um aumento na variável Y. A pouca dispersão dos dados indica que essa tendência é forte;
- Correlação positiva média: quando a variável X sobe, a variável Y tende a subir também. Entretanto, a dispersão maior dos dados indica que mais variáveis podem estar envolvidas. Adicionar outras variáveis, como variáveis de estratificação, ou testar medições alternativas de X podem ser uma boa estratégia para se entender melhor a correlação;
- Correlação negativa forte: análoga à correlação positiva forte, só que quando X aumenta, Y diminui;
- Correlação negativa média: análoga à correlação positiva média, porém quando X aumenta, Y diminui.
Como interpretar o gráfico de dispersão?
Identificar a direção da relação
É possível identificar se a relação entre as variáveis é positiva (os valores de uma variável aumentam quando os valores da outra variável aumentam), negativa (os valores de uma variável diminuem quando os valores da outra variável aumentam) ou não existe relação aparente.
Identificar a forma da relação
Em alguns casos, a relação entre as variáveis pode ser linear (os pontos formam uma linha reta), em outros casos a relação pode ser não-linear (os pontos não formam uma linha reta). Em casos não-lineares, é importante identificar a forma da curva, pois pode fornecer informações valiosas sobre a relação entre as variáveis.
Identificar a força da relação
A dispersão dos pontos pode fornecer uma indicação da força da relação entre as variáveis. Se os pontos estão próximos uns dos outros, a relação é considerada forte. Se os pontos estão espalhados, a relação é considerada fraca.
Identificar valores discrepantes
É importante observar se há valores discrepantes (outliers) no gráfico. Esses pontos podem ter um impacto significativo na análise estatística e podem indicar a presença de erros ou problemas nos dados.